Multi-Fidelity Random Embedding Bayesian Optimization
Overview
Bayesian optimization is a sample-efficient approach to optimizing expensive-to-evaluate black-box functions, particularly when observations are noisy. However, standard methods suffer from the curse of dimensionality—performance degrades rapidly for problems with more than ~20 parameters.
This research extends random embedding Bayesian optimization to leverage multi-fidelity information sources and introduces a novel embedding selection strategy based on multi-armed bandit algorithms. These advances enable efficient optimization of high-dimensional problems by exploiting low effective dimensionality while reducing computational cost through intelligent use of cheap approximations.
Random Embeddings
Many high-dimensional optimization problems have low effective dimensionality—the objective function varies primarily within an unknown low-dimensional subspace. Random embedding methods exploit this structure by optimizing within randomly-oriented low-dimensional linear subspaces of the original space.
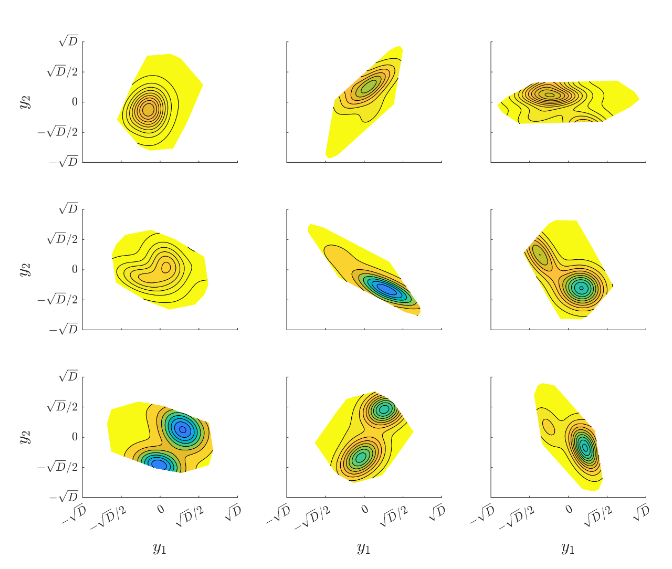
Nine random embeddings with dimension de = 2 of a 6-dimensional test function. Each embedding reveals a different 2D slice through the high-dimensional landscape. Linear constraints define polytope-shaped feasible regions that avoid nonlinearities from projecting points back to the original domain.
By maintaining multiple embeddings and using a geometry-aware Mahalanobis kernel, the algorithm can efficiently explore the high-dimensional space while building accurate surrogate models within each low-dimensional subspace.
Key Contributions
Multi-Fidelity Extension
Extended the ALEBO algorithm to incorporate observations at multiple fidelity levels using an autoregressive Gaussian process model, enabling use of cheap approximations to guide expensive evaluations.
Bandit-Based Selection
Introduced a contextual multi-armed bandit formulation for embedding selection using Thompson sampling, balancing exploration of uncertain embeddings with exploitation of promising ones.
Sample Efficiency
Achieved significant reduction in required high-fidelity evaluations by intelligently allocating samples across fidelity levels and embeddings based on expected improvement.
Multi-Fidelity Modeling
The multi-fidelity approach models the relationship between cheap approximations and expensive ground truth using an autoregressive structure. The high-fidelity function is expressed as a scaled version of the low-fidelity function plus a learned discrepancy:
This formulation allows information from many inexpensive evaluations to inform the surrogate model, reducing the number of costly high-fidelity samples needed to find the optimum. The correlation coefficient and discrepancy function are learned jointly by maximizing the log marginal likelihood.
Embedding Selection as a Bandit Problem
When maintaining multiple random embeddings, a key question is which embedding to sample next. Sequential cycling through embeddings can waste evaluations on subspaces that don't contain the optimum.
By formulating embedding selection as a multi-armed bandit problem, the algorithm learns which embeddings are most promising. A reward function combining immediate improvement with expected improvement guides Thompson sampling to balance:
- Exploitation: Focusing samples on embeddings that have yielded good solutions
- Exploration: Sampling uncertain embeddings that may contain undiscovered optima
Applications
This framework applies to any expensive-to-evaluate optimization problem with many parameters but suspected low effective dimensionality:
- Engineering Design: Aerodynamic shape optimization, structural design, materials discovery
- Hyperparameter Tuning: Neural network architecture search, algorithm configuration
- Scientific Computing: Calibration of simulation parameters, surrogate-based optimization
- Experimental Design: Sequential experimental optimization with costly physical tests